Intellectually, we know details and small differences matter. We can see the slight differences between two products that look similar on the surface but one is merely functional and the other is delightful. We can hear the differences between two orchestras playing the same notes, yet one rendition makes you yawn, and the other gives you goosebumps. At Zappos, we were fascinated by how to take the ordinary to the extraordinary. Our observation was that consistently making small improvements is what it takes to be extraordinary. This requires more effort every day but surprisingly little additional effort than required for ordinary results because the answer lies in consistent compounding.

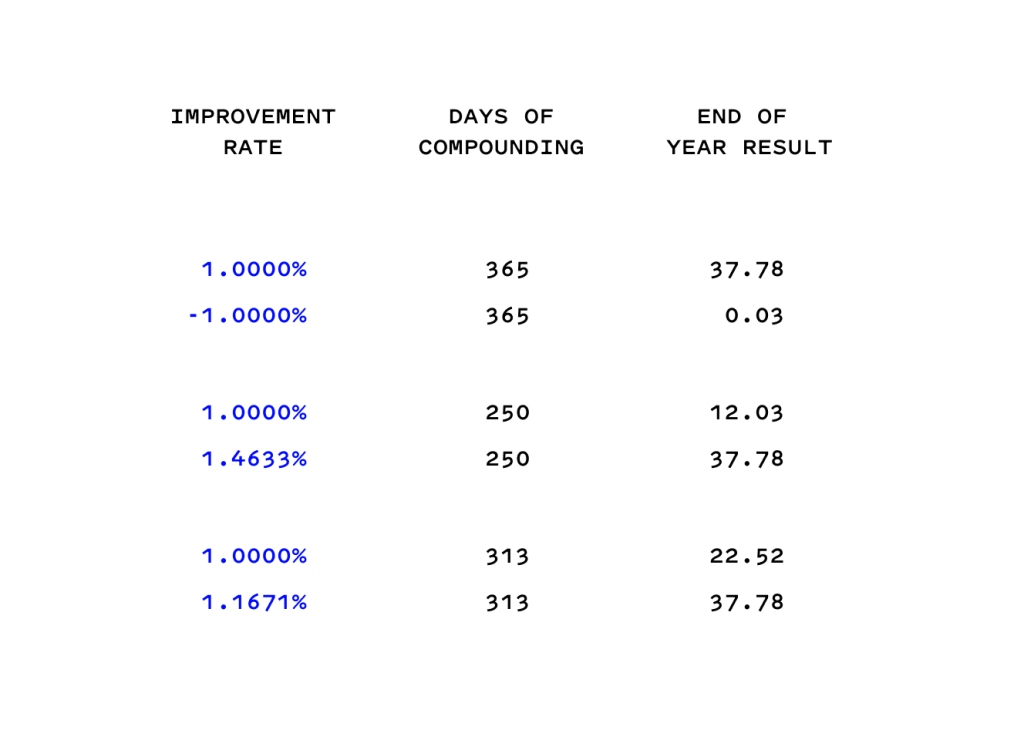
Consistent compounding is one of the most powerful concepts we believe we understand but do not. Many of you know I love the mathematical expression (1 + 1%)^365 = 37.78. If you start out with $100 at the beginning of the year and can consistently compound 1% every day, you’ll have $3778, which is 37.78x! Compounding is also powerful in the opposite direction, as (1 – 1%)^365 = 0.03, which means you are left with almost nothing!

At Zappos, we memorialized these lessons as the Power of 1%. We compounded that power into fulfillment operations that operated 30% more efficiently than an Amazon fulfillment center at the time of acquisition. Amazon would later acquire Kiva Systems because of how well its robots operated in the Zappos fulfillment center.

Another example that highlights that we do not understand compounding is the proclamation by many founders that their financial performance is on plan, so how could their company’s valuation fall by 80%? My simple retort is to ask them to take their ten-year free cash flow projections and calculate the net present value of those projections. This is an example of a company, similar to many of our companies, which starts out investing in its business with its free cash generation in the later years.

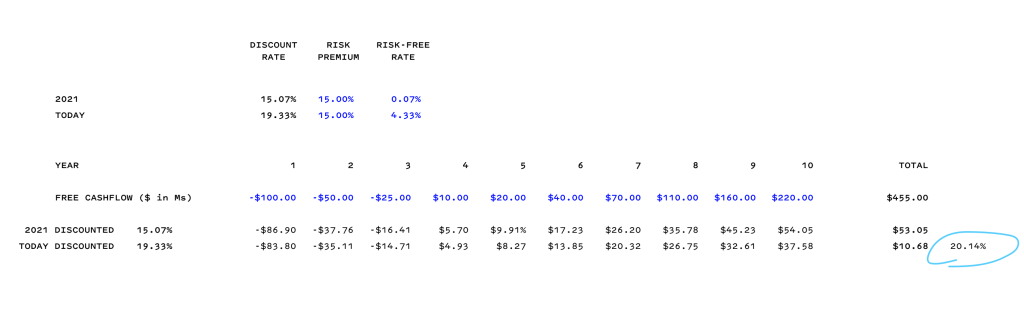
We assume a risk-premium rate of 15% and use the Fed Funds rate to approximate the risk-free rate. *Today’s effective Fed Fund rate is 4.33% vs. 0.07% in 2021. The discounted cash flows today are worth only ~20% of what it was worth in 2021. Q.E.D.

The moral of the story is to think slow and do the simple math. More importantly, we should put into practice making small improvements every single day in whatever we choose to do. Making small improvements, such as a 1% improvement, is achievable, so we have no excuse. Making small improvements consistently is difficult because consistency requires discipline. Making small improvements compounded daily is extremely hard, but it is essential in our pursuit of excellence.

Our goal should not be a destination of perfection because it doesn’t exist. We “pursue” excellence because we will never achieve excellence, as the bar will always be raised. Our goal is to find joy in the process of consistent and never-ending improvement. As Pat Grady would say, “get better at getting better.” To that end, what is your 1% improvement today? Will you commit to finding a 1% improvement every day? Will you find joy in this process? If we do, there is no doubt that our results will be extraordinary. In the meantime, let’s go…or as Ravi Gupta would say…”LFG!”

P. S. If you want the same results of compounding 1% improvement every day of a year but only want to compound on the 250 work days, you have to compound at 1.4633%. Feel free to work hard and play hard. If you want to work six days a week rather than seven days a week, you have to compound at 1.1671% to get the same results. The backup math is below.

*The effective Fed Funds rate on January 8, 2023.